为丰富课余生活，某班开展了一次有奖知识竞赛，在竞赛后把成绩（满分为100分，分数均为整数）进行统计，制成如图的频率分布表：
（Ⅰ）求
的值；
（Ⅱ）若得分在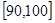
之间的有机会得一等奖，已知其中男女比例为2∶3，如果一等奖只有两名，写出所有可能的结果，并求获得一等奖的全部为女生的概率.
相关试题
。
，若
，求集合A；
是
的必要不充分条件，求
的取值范围.
和
，且
.
，
的表达式；
时，不等式
在
上恒成立，求实数
的取值范围.
和
．其中
．
与
的图像的一个公共点恰好在
轴上，求
的值；
和
是方程
的两根，且满足
，证明：当
时，
．
.
时，求曲线
在点
处的切线方程；
，且
，求函数
的单调区间.
的函数
（
为实数）。
是奇函数，求
都有
成立.推荐套卷
为丰富课余生活，某班开展了一次有奖知识竞赛，在竞赛后把成绩（满分为100分，分数均为整数）进行统计，制成如图的频率分布表：
（Ⅰ）求的值；
（Ⅱ）若得分在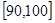之间的有机会得一等奖，已知其中男女比例为2∶3，如果一等奖只有两名，写出所有可能的结果，并求获得一等奖的全部为女生的概率.
粤公网安备 44130202000953号