已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球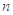
个.若从袋子中随机抽取1个小球，取到标号为2的小球的概率为
.
（1）求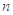的值；
（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球的标号为
，第二次取出的小球的标号为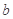
,记“a+b=2”为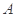事件
，求事件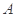的概率.
的不等式
。
内一点A(1，－1)为中点的弦所在直线的方程。
，当实数
为何值时。
为实数；
中，
，设
是等差数列，并求其通项公式；
的值，使得
的周期为
，求
的值；
上为增函数，求满足条件的整数推荐套卷
已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球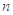个.若从袋子中随机抽取1个小球，取到标号为2的小球的概率为.
（1）求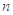的值；
（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球的标号为，第二次取出的小球的标号为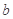,记“a+b=2”为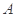事件，求事件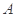的概率.
粤公网安备 44130202000953号