已知函数f（x）=（x+a）2+lnx．
（1）当a=
时，求函数f（x）在[1，+∞）上的最小值；
（2）若函数f（x）在[2，+∞）上递增，求实数a的取值范围；
（3）若函数f（x）有两个极值点x1、x2，且x1∈（0，
），证明：f（x1）﹣f（x2）＞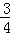
﹣ln2．
，
，
经过点
，
，当直线
与
的值．
，
，
三点，求点
，使直线
，且
．
，
，
三点，这三点是否在同一条直线上，为什么？
，
，
，
是这条直线上的三个点，求
和
的值．
，
，
三点，试判断
的形状．推荐套卷
已知函数f（x）=（x+a）2+lnx．
（1）当a=时，求函数f（x）在[1，+∞）上的最小值；
（2）若函数f（x）在[2，+∞）上递增，求实数a的取值范围；
（3）若函数f（x）有两个极值点x1、x2，且x1∈（0，），证明：f（x1）﹣f（x2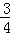）＞﹣ln2．
粤公网安备 44130202000953号