（本小题满分13分）有20名学生参加某次考试，成绩（单位：分）的频率分布直方图如图所示：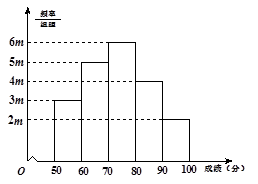
（1）求频率分布直方图中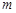
的值；
（2）分别求出成绩落在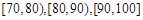
中的学生人数；
（3）从成绩在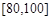
的学生中任选2人，求所选学生的成绩都落在
中的概率．
相关试题
.
的单调区间；
，求
上的最大值；
，不等式
恒成立．
，
．
在
上的值域；
2）若对于任意
，总存在
，使得
成立，求
的取值范围．
，若
图象上的点
处的切线斜率为
，求
上的最值.
12分）
(
），比较
、
、
的大小，并证明你的结论
，函数
的两个零点为
.
求不等式
的解集；
且
，比较
与
的大小．推荐套卷
（本小题满分13分）有20名学生参加某次考试，成绩（单位：分）的频率分布直方图如图所示：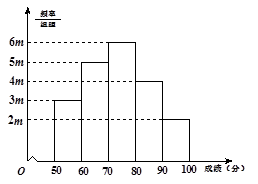
（1）求频率分布直方图中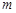的值；
（2）分别求出成绩落在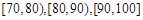中的学生人数；
（3）从成绩在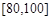的学生中任选2人，求所选学生的成绩都落在中的概率．
粤公网安备 44130202000953号