在Rt△ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=
．
（1）如图，当点E在边AC上时，点E不与点A、C重合，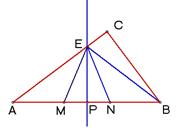
①求证：△AEP∽△ABC
②设AP=x，求MP的长 （用含x的代数式表示）
（2）若△AME∽△ENB，求AP的长．
，
，求当x取何值时，
的值比
的值小1？
的解是非负数，求m的取值范围．
，并把解集在数轴上表示出来．
．
相关知识点
推荐套卷
在Rt△ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=．
（1）如图，当点E在边AC上时，点E不与点A、C重合，
①求证：△AEP∽△ABC
②设AP=x，求MP的长 （用含x的代数式表示）
（2）若△AME∽△ENB，求AP的长．
粤公网安备 44130202000953号