如图，在△ABC中，∠ABC=45º，CD⊥AB，BE⊥AC，垂足分别为D、E，F为BC中点，BE与DF、DC分别交于点G、H，∠ABE=∠CBE。
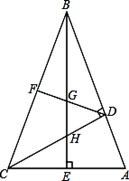
（1）线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；
（2）求证：
相关试题
,
,AD是△ABC的角平分线，求
的度数.
相关知识点
推荐套卷
如图，在△ABC中，∠ABC=45º，CD⊥AB，BE⊥AC，垂足分别为D、E，F为BC中点，BE与DF、DC分别交于点G、H，∠ABE=∠CBE。
（1）线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；
（2）求证：
粤公网安备 44130202000953号