（本小题满分13分）设关于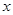
的一元二次方程
.
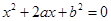（1）若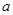
是从
、
、
、
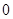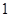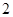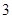四个数中任取的一个数，
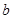是从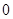、、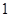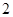三个数中任取的一个数，求上述方程有实根的概率；
（2）若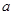
是从区间
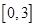任取的一个数，
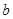是从区间
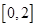任取的一个数，求上述方程有实根的概率.
与
互相平行，且
，
之间的距离为
，求直线
，点
，求证：
，且平行于直线
的直线方程是
；
．
，
到直线
的距离相等，求
的值．
，
，
，求
的面积．
与
的交点坐标．推荐套卷
（本小题满分13分）设关于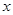的一元二次方程.
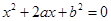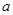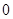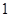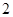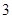（1）若是从、、、四个数中任取的一个数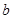，是从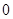、、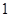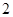三个数中任取的一个数，求上述方程有实根的概率；
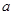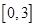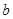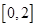（2）若是从区间任取的一个数，是从区间任取的一个数，求上述方程有实根的概率.
粤公网安备 44130202000953号