如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：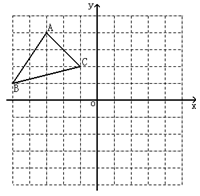
（1）将△ABC向右平移3个单位长度再向下平移2个单位长度，画出两次平移后的△A1B1C1；
（2）写出A1、C1的坐标；
（3）将△A1B1C1绕C1逆时针旋转90°，画出旋转后的△A2B2C1，求线段B1C1旋转过程中扫过的面积（结果保留
）．
，其中
，
。
的解是
，求
的值.
相关知识点
推荐套卷
如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
（1）将△ABC向右平移3个单位长度再向下平移2个单位长度，画出两次平移后的△A1B1C1；
（2）写出A1、C1的坐标；
（3）将△A1B1C1绕C1逆时针旋转90°，画出旋转后的△A2B2C1，求线段B1C1旋转过程中扫过的面积（结果保留）．
粤公网安备 44130202000953号