.已知圆 :x2+y2-2x-2y-2=0.
:x2+y2-2x-2y-2=0.
(1)若直线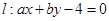 平分圆
平分圆 的周长,求原点O到直线
的周长,求原点O到直线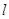 的距离的最大值;
的距离的最大值;
(2)若圆 平分圆
平分圆 的周长,圆心
的周长,圆心 在直线y=2x上,求符合条件且半径最小的圆B的方程.
在直线y=2x上,求符合条件且半径最小的圆B的方程.
相关知识点
推荐套卷
.已知圆 :x2+y2-2x-2y-2=0.
:x2+y2-2x-2y-2=0.
(1)若直线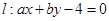 平分圆
平分圆 的周长,求原点O到直线
的周长,求原点O到直线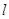 的距离的最大值;
的距离的最大值;
(2)若圆 平分圆
平分圆 的周长,圆心
的周长,圆心 在直线y=2x上,求符合条件且半径最小的圆B的方程.
在直线y=2x上,求符合条件且半径最小的圆B的方程.