(本题10分)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点。
(1)求线段MN的长;
(2)若C为线段AB上任意一点,满足AC+CB=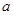 cm,其他条件不变,你能猜想MN的长度吗?并说明理由。
cm,其他条件不变,你能猜想MN的长度吗?并说明理由。
(3)若C在AB的延长线上,且满足AC-CB=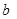 cm,其他条件不变, MN的长度
cm,其他条件不变, MN的长度
为 。(直接写出答案)
(本题10分)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点。
(1)求线段MN的长;
(2)若C为线段AB上任意一点,满足AC+CB=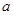 cm,其他条件不变,你能猜想MN的长度吗?并说明理由。
cm,其他条件不变,你能猜想MN的长度吗?并说明理由。
(3)若C在AB的延长线上,且满足AC-CB=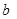 cm,其他条件不变, MN的长度
cm,其他条件不变, MN的长度
为 。(直接写出答案)