操作与探究
我们知道：过任意一个三角形的三个顶点能作一个圆，探究过四边形四个顶点作圆的条件。
（1）分别测量下面各四边形的内角，如果过某个四边形的四个顶点能一个圆，那么其相对的两个角之间有什么关系？证明你的发现.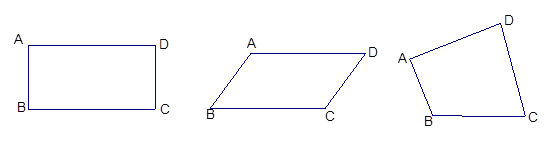
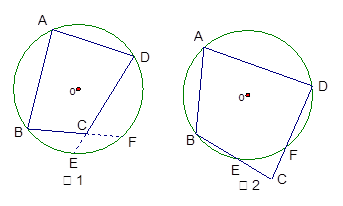
(2) 如果过某个四边形的四个顶点不能一个圆，那么其相对的两个角之间有上面的关系吗？试结合下面的两个图说明其中的道理.（提示：考虑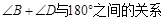
）
由上面的探究，试归纳出判定过四边形的四个顶点能作一个圆的条件.
元/千克，第二次的价格为
元/千克，两位采购员的购货方式也不同：甲每次购买800千克；乙每次用去600元，而不管购买多少肥料．相关知识点
推荐套卷
操作与探究
我们知道：过任意一个三角形的三个顶点能作一个圆，探究过四边形四个顶点作圆的条件。
（1）分别测量下面各四边形的内角，如果过某个四边形的四个顶点能一个圆，那么其相对的两个角之间有什么关系？证明你的发现.
(2) 如果过某个四边形的四个顶点不能一个圆，那么其相对的两个角之间有上面的关系吗？试结合下面的两个图说明其中的道理.（提示：考虑）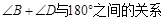
由上面的探究，试归纳出判定过四边形的四个顶点能作一个圆的条件.
粤公网安备 44130202000953号