如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.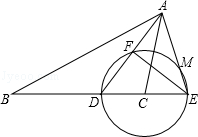
(1)求证:点F是AD的中点;
(2)求cos∠AED的值;
(3)如果BD=10,求半径CD的长.
推荐套卷
如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.
(1)求证:点F是AD的中点;
(2)求cos∠AED的值;
(3)如果BD=10,求半径CD的长.