（满分12分）已知圆O：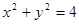
，点P在直线
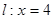上的动点。
（1）若从P到圆O的切线长为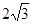
，求P点的坐标以及两条切线所夹劣弧长；
（2）若点A（-2，0），B（2，0），直线PA，PB与圆O的另一个交点分别为M，N，求证：直线MN经过定点（1，0）。
表示两条直线,求m的值
+(x-1)0 ; 
);(3)y=f(
; (4)y=f(x+a)+f(x-a).
+lgcosx;相关知识点
推荐套卷
（满分12分）已知圆O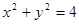：，点P在直线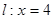上的动点。
（1）若从P到圆O的切线长为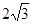，求P点的坐标以及两条切线所夹劣弧长；
（2）若点A（-2，0），B（2，0），直线PA，PB与圆O的另一个交点分别为M，N，求证：直线MN经过定点（1，0）。
粤公网安备 44130202000953号