（本小题满分12分）如图，为测得河对岸某建筑物AB的高，先在河岸上选一点C，使C在建筑物底端B的正东方向上，测得点A的仰角为α，再由点C沿东偏北β（β<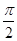
）角方向走d米到达位置D，测得∠BDC=γ．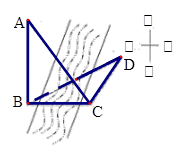
（Ⅰ）若β=75°，求sⅠn∠BCD的值；
（Ⅱ）求此建筑物的高度（用字母表示）．
相关试题
中，
面
,
为菱形，且有
，
,∠
,
为
中点.
面
；
的平面角的余弦值.
是等差数列，且
，
.
，求数列
前
项和公式
：关于
的不等式
的解集为空集
；命题
：函数
没有零点，若命题
为假命题，
为真命题，求实数
的取值范围.
，且与椭圆
有相同的焦距，求双曲线的标准方程
中，内角
的对边分别是
，且
，
, 
,求边长
和
相关知识点
推荐套卷
（本小题满分12分）如图，为测得河对岸某建筑物AB的高，先在河岸上选一点C，使C在建筑物底端B的正东方向上，测得点A的仰角为α，再由点C沿东偏北β（β<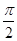）角方向走d米到达位置D，测得∠BDC=γ．
（Ⅰ）若β=75°，求sⅠn∠BCD的值；
（Ⅱ）求此建筑物的高度（用字母表示）．
粤公网安备 44130202000953号