(本小题满分15分)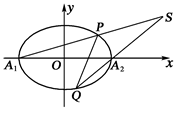
已知椭圆C的离心率e=,长轴的左右端点分别为A1(-2,0),A2(2,0).
(I)求椭圆C的方程;
(II)设直线x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
推荐套卷
(本小题满分15分)
已知椭圆C的离心率e=,长轴的左右端点分别为A1(-2,0),A2(2,0).
(I)求椭圆C的方程;
(II)设直线x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.