已知正方形A BCD中，BE平分∠DBC且交CD边于点E，将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G。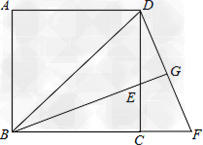
（1）求证：△BDG∽△DEG。
（2）若EG•BG=4，求BE的长。
相关试题
．
，求作△ABC，使得BC = a，AC = b，
．（不写作法，保留作图痕迹）．
；
；
……
相关知识点
推荐套卷
已知正方形A BCD中，BE平分∠DBC且交CD边于点E，将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G。
（1）求证：△BDG∽△DEG。
（2）若EG•BG=4，求BE的长。
粤公网安备 44130202000953号