我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
(2)如图(1),已知格点(小正方形的顶点)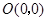 ,
,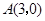 ,
,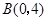 ,请你画出以格点为顶点,
,请你画出以格点为顶点,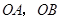 为勾股边且对角线相等的非长方形的勾股四边形
为勾股边且对角线相等的非长方形的勾股四边形 ;并写出点M的坐标.
;并写出点M的坐标.
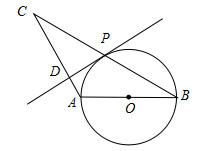
(3)如图(2),将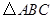 绕顶点
绕顶点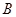 按顺时针方向旋转
按顺时针方向旋转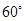 ,得到
,得到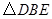 ,连结
,连结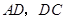 ,已知
,已知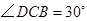 .求证:
.求证: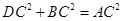 ,即四边形
,即四边形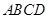 是勾股四边形.
是勾股四边形.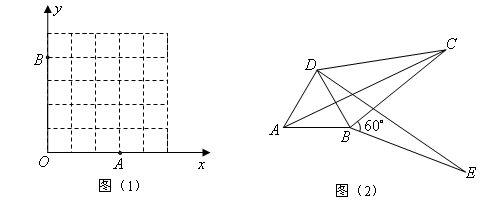
相关知识点
推荐套卷
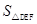 +
+ =
=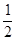
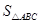 .
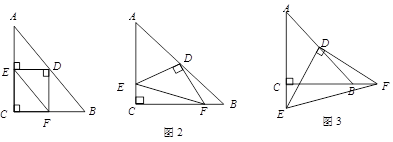
. 当∠EDF绕
当∠EDF绕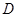 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,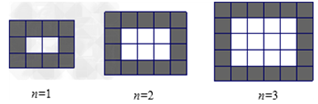
 粤公网安备 44130202000953号
粤公网安备 44130202000953号