如图,点 为 轴负半轴上的一个点,过点 作 轴的垂线,交函数 的图象于点 ,交函数 的图象于点 ,过点 作 轴的平行线,交 于点 ,连接 .
(1)当点 的坐标为 时,求 的面积;
(2)若 ,求点 的坐标;
(3)连接 和 .当点 的坐标为 时, 的面积是否随 的值的变化而变化?请说明理由.
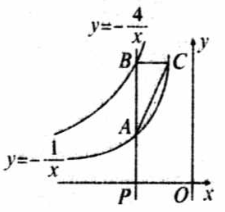
如图,点 为 轴负半轴上的一个点,过点 作 轴的垂线,交函数 的图象于点 ,交函数 的图象于点 ,过点 作 轴的平行线,交 于点 ,连接 .
(1)当点 的坐标为 时,求 的面积;
(2)若 ,求点 的坐标;
(3)连接 和 .当点 的坐标为 时, 的面积是否随 的值的变化而变化?请说明理由.
