(本小题满分15分)平面直角坐标系xOy中,已知以M为圆心的圆M经过点F1(0,-c),F2(0,c),A(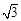 c,0)三点,其中c>0.
c,0)三点,其中c>0.
(1)求圆M的标准方程(用含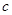 的式子表示);
的式子表示);
(2)已知椭圆 (其中
(其中 )的左、右顶点分别为D、B,圆M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
)的左、右顶点分别为D、B,圆M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
推荐套卷
 :
: ;(2)至少有一个实数
;(2)至少有一个实数 ,使得
,使得 。
。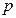 :
: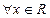 ,
,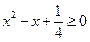 ;(2)
;(2) :所有的正方形都是矩形;
:所有的正方形都是矩形; :对一切
:对一切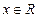 ,都有
,都有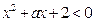 ,若
,若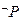 为真,求实数
为真,求实数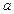 的取值范围。
的取值范围。 的定义域是
的定义域是 ,且满足
,且满足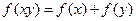 ,
,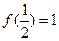 ,如果对于
,如果对于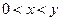 ,都有
,都有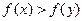 ,(1)求
,(1)求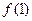 ;(2)解不等式
;(2)解不等式
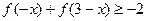 。
。 为实数,函数
为实数,函数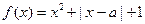 ,
,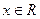
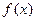 的奇偶性;
的奇偶性; 粤公网安备 44130202000953号
粤公网安备 44130202000953号