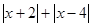(本题12分)阅读下列材料并解决有关问题:我们知道 ,现在我们可以用这一个结论来化简含有绝对值的代数式,如化简代数式
,现在我们可以用这一个结论来化简含有绝对值的代数式,如化简代数式 时,可令
时,可令 和
和 ,分别求得
,分别求得 (称
(称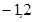 分别为
分别为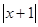 与
与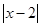 的零点值).在有理数范围内,零点值
的零点值).在有理数范围内,零点值 和
和 可将全体有理数分成不重复且不遗漏的如下3种情况:(1)当
可将全体有理数分成不重复且不遗漏的如下3种情况:(1)当 时,原式=
时,原式= ;
;
(2)当 时,原式=
时,原式= ;
;
(3)当 时,原式=
时,原式= .
.
综上讨论,原式=
通过以上阅读,请你解决以下问题:(1)求出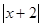 和
和 的零点值;(2)化简代数式
的零点值;(2)化简代数式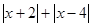
相关知识点
推荐套卷
(本题12分)阅读下列材料并解决有关问题:我们知道 ,现在我们可以用这一个结论来化简含有绝对值的代数式,如化简代数式
,现在我们可以用这一个结论来化简含有绝对值的代数式,如化简代数式 时,可令
时,可令 和
和 ,分别求得
,分别求得 (称
(称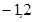 分别为
分别为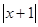 与
与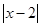 的零点值).在有理数范围内,零点值
的零点值).在有理数范围内,零点值 和
和 可将全体有理数分成不重复且不遗漏的如下3种情况:(1)当
可将全体有理数分成不重复且不遗漏的如下3种情况:(1)当 时,原式=
时,原式= ;
;
(2)当 时,原式=
时,原式= ;
;
(3)当 时,原式=
时,原式= .
.
综上讨论,原式=
通过以上阅读,请你解决以下问题:(1)求出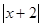 和
和 的零点值;(2)化简代数式
的零点值;(2)化简代数式