已知定理:“若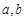 为常数,
为常数,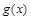 满足
满足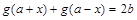 ,则函数
,则函数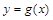 的图象关于点
的图象关于点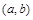 中心对称”.设函数
中心对称”.设函数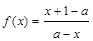 ,定义域为A.
,定义域为A.
(1)试证明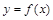 的图象关于点
的图象关于点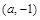 成中心对称;
成中心对称;
(2)当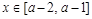 时,求证:
时,求证: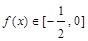 ;
;
(3)对于给定的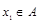 ,设计构造过程:
,设计构造过程: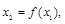
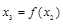 ,…,
,…,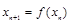 .如果
.如果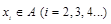 ,构造过程将继续下去;如果
,构造过程将继续下去;如果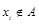 ,构造过程将停止.若对任意
,构造过程将停止.若对任意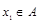 ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.
相关知识点
推荐套卷
已知定理:“若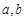 为常数,
为常数,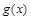 满足
满足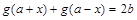 ,则函数
,则函数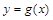 的图象关于点
的图象关于点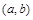 中心对称”.设函数
中心对称”.设函数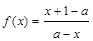 ,定义域为A.
,定义域为A.
(1)试证明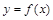 的图象关于点
的图象关于点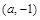 成中心对称;
成中心对称;
(2)当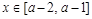 时,求证:
时,求证: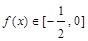 ;
;
(3)对于给定的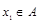 ,设计构造过程:
,设计构造过程: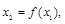
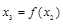 ,…,
,…,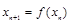 .如果
.如果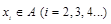 ,构造过程将继续下去;如果
,构造过程将继续下去;如果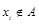 ,构造过程将停止.若对任意
,构造过程将停止.若对任意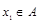 ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.