（本小题满分14分）已知A，B分别是直线y＝x和y＝－x上的两个动点，线段AB的长为2
，D是AB的中点．
（Ⅰ）求动点D的轨迹C的方程；
（Ⅱ）若过点(1,0)的直线l与曲线C交于不同两点P、Q，
① 当|PQ|＝3时，求直线l的方程；
② 试问在x轴上是否存在点E(m,0)，使
·
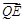恒为定值？若存在，求出E点的坐标及定值；若不存在，请说明理由．
相关试题
逆时针方向转90°到QH，
的最值
，定点F（10，4），对于x轴上移动的点P（t，0）作一折线FPQ，使
，若折线FPQ的PQ部分与正方形ABCD的边界有公共点，推荐套卷
（本小题满分14分）已知A，B分别是直线y＝x和y＝－x上的两个动点，线段AB的长为2，D是AB的中点．
（Ⅰ）求动点D的轨迹C的方程；
（Ⅱ）若过点(1,0)的直线l与曲线C交于不同两点P、Q，
① 当|PQ|＝3时，求直线l的方程；
② 试问在x轴上是否存在点E(m,0)，使·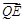恒为定值？若存在，求出E点的坐标及定值；若不存在，请说明理由．
粤公网安备 44130202000953号