(本小题满分14分)
已知二次函数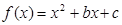 的图象过点
的图象过点 ,且函数对称轴方程为
,且函数对称轴方程为 .
.
(Ⅰ)求函数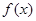 的解析式;
的解析式;
(Ⅱ)设函数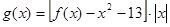 ,求
,求 在区间
在区间 上的最小值
上的最小值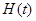 ;
;
(Ⅲ)探究:函数 的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
相关知识点
推荐套卷
(本小题满分14分)
已知二次函数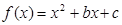 的图象过点
的图象过点 ,且函数对称轴方程为
,且函数对称轴方程为 .
.
(Ⅰ)求函数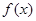 的解析式;
的解析式;
(Ⅱ)设函数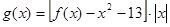 ,求
,求 在区间
在区间 上的最小值
上的最小值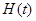 ;
;
(Ⅲ)探究:函数 的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.