（本小题满分12分）
已知函数
的定义域是
，对于任意的
，有
，且当
时，
．
（Ⅰ）验证函数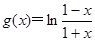
是否满足上述这些条件；
（Ⅱ）你发现这样的函数还具有其它什么样的主要性质？试就函数的奇偶性、单调性的结论写出来，并加以证明．
，求证：
不可能都是奇数
有相同焦点，且经过点
，求双曲线的方程
所表示的曲线.
的实轴和虚轴的长、顶点和焦点
坐标、离心率、渐近线方程：推荐套卷
（本小题满分12分）
已知函数的定义域是，对于任意的，有，且当时，．
（Ⅰ）验证函数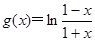是否满足上述这些条件；
（Ⅱ）你发现这样的函数还具有其它什么样的主要性质？试就函数的奇偶性、单调性的结论写出来，并加以证明．
粤公网安备 44130202000953号