通过研究学生的学习行为,专家发现,学生的注意力随老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设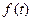 表示学生的注意力随时间
表示学生的注意力随时间 (分钟)的变化规律(注:
(分钟)的变化规律(注: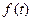 越大,表明学生的注意力越集中),经过实验分析得知:
越大,表明学生的注意力越集中),经过实验分析得知: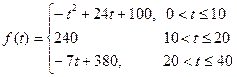 .
.
(1).讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2).讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3).一道数学难题需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?