从某校高三学生中抽取 名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40, 100),且成绩在区间[70, 90)的学生人数是27人.
名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40, 100),且成绩在区间[70, 90)的学生人数是27人.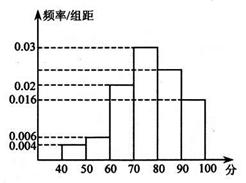
(1)求 的值;
的值;
(2)若从数学成绩(单位:分)在[40,60)的学生中随机选取2人进行成绩分析,求至少有1人成绩在[40, 50)内的概率.
推荐套卷
从某校高三学生中抽取 名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40, 100),且成绩在区间[70, 90)的学生人数是27人.
名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40, 100),且成绩在区间[70, 90)的学生人数是27人.
(1)求 的值;
的值;
(2)若从数学成绩(单位:分)在[40,60)的学生中随机选取2人进行成绩分析,求至少有1人成绩在[40, 50)内的概率.