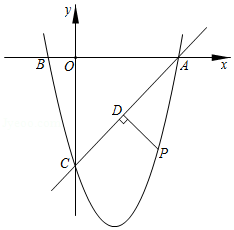
如图，抛物线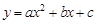
交x轴于点A（－3，0），点B（1，0），交y轴于点E（0，－3）．点C是点A关于点B的对称点，点F是线段BC的中点，直线l过点F且与y轴平行．直线
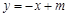过点C，交y轴于D点．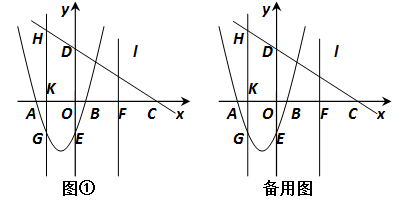
（1）求抛物线的函数表达式；
（2）点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于点G，求线段HG长度的最大值；
（3）在直线l上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边形是平行四边形，求点N的坐标．
相关试题
、
、
、
四点在一直线上，AF=CD，AB∥DE，且AB=DE，求证：△ABC≌△DEF．
如图，已知直线l的函数表达式为
，且l与x轴、y轴分别交于A、B两点，动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动，同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动，设点Q、P移动时间为t秒。
（1）求点A、B的坐标。
（2）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？
；相关知识点
推荐套卷
粤公网安备 44130202000953号