已知关于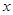
的一元二次方程
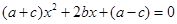，其中
、
、
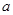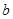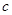分别为△ABC三边的长．
（1）如果
是方程的根，试判断△ABC的形状，并说明理由：
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
相关知识点
推荐套卷
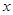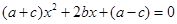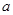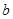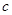已知关于的一元二次方程，其中、、分别为△ABC三边的长．
（1）如果是方程的根，试判断△ABC的形状，并说明理由：
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
粤公网安备 44130202000953号