（本小题满分13分）如图是学校从走读生中随机调查200名走读生早上上学所需时间（单位：分钟）样本的频率分布直方图．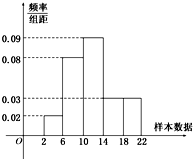
（1）学校所有走读生早上上学所需要的平均时间约是多少分钟？
（2）根据调查，距离学校500米以内的走读生上学时间不超过10分钟，距离学校1000米以内的走读生上学时间不超过20分钟．那么，距离学校500米以内的走读生和距离学校1000米以上的走读生所占全校走读生的百分率各是多少？
相关试题
与
，
，
所围成的平面图形的面积(画出图形)。
的二项展开式中所有奇数项的系数之和为512，
展开式中
项的系数．
，其中
时，求
的最大值、最小值。
的取值范围，使
在区间上
是单调函数。
的最小正周期。
的解集。
的图象怎样变换得到？相关知识点
推荐套卷
粤公网安备 44130202000953号