（本小题满分12分）边长为2的正方形ABCD中,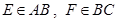 
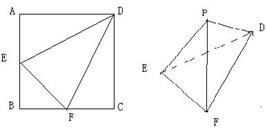
（1）如果E、F分别为AB、BC中点, 分别将△AED、△DCF、△BEF沿ED、DF、FE折起, 使A、B、C重合于点P.证明: 在折叠过程中, A点始终在某个圆上, 并指出圆心和半径.
（2）如果F为BC的中点, E是线段AB上的动点, 沿DE、DF将△AED、△DCF折起,使A、
C重合于点P, 求三棱锥P－DEF体积的最大值.
在曲线
的距离最小，求出该点坐标和最小距离
的值；②求
的逆矩阵
，求函数
的最小值
时，求函数
的定义域；
，试求
的取值范围
被选中的概率；
和
不全被选中的概率相关知识点
推荐套卷
（本小题满分12分）边长为2的正方形ABCD中,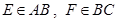
（1）如果E、F分别为AB、BC中点, 分别将△AED、△DCF、△BEF沿ED、DF、FE折起, 使A、B、C重合于点P.证明: 在折叠过程中, A点始终在某个圆上, 并指出圆心和半径.
（2）如果F为BC的中点, E是线段AB上的动点, 沿DE、DF将△AED、△DCF折起,使A、
C重合于点P, 求三棱锥P－DEF体积的最大值.
粤公网安备 44130202000953号