（本小题满分12分）下图是调查某地某公司1000名员工的月收入后制作的直方图.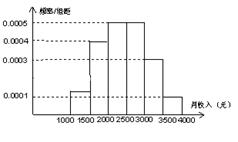
（1）求该公司员工的月平均收入及员工月收入的中位数;
（2）在收入为1000至1500元和收入为3500至4000元的员工中用分层抽样的方法抽取一个容量15的样本, 员工甲、乙的月收入分别为1200元、3800元, 求甲乙同时被抽到的概率.
相关试题
x2dx的值．
xdx； (2)
cos xdx.相关知识点
推荐套卷
（本小题满分12分）下图是调查某地某公司1000名员工的月收入后制作的直方图.
（1）求该公司员工的月平均收入及员工月收入的中位数;
（2）在收入为1000至1500元和收入为3500至4000元的员工中用分层抽样的方法抽取一个容量15的样本, 员工甲、乙的月收入分别为1200元、3800元, 求甲乙同时被抽到的概率.
粤公网安备 44130202000953号