问题探究(本题10分):
(1)请在图①的正方形ABCD内,画出使∠APB=90°的一个点,并说明理由.
(2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,
并说明理由.
问题解决:
(3)如图③,现在一块矩形钢板ABCD,AB=4,BC=3.工人师傅想用它
裁出两块全等的.面积最大的△APB和△CP'D钢板,且∠APB=∠CP'D=60°.
请你在图③中画出符合要求的点和P和P'.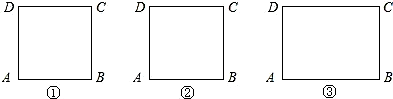
推荐套卷
问题探究(本题10分):
(1)请在图①的正方形ABCD内,画出使∠APB=90°的一个点,并说明理由.
(2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,
并说明理由.
问题解决:
(3)如图③,现在一块矩形钢板ABCD,AB=4,BC=3.工人师傅想用它
裁出两块全等的.面积最大的△APB和△CP'D钢板,且∠APB=∠CP'D=60°.
请你在图③中画出符合要求的点和P和P'.