如图,⊙O的直径AB为10,弦BC为6,D、E分别为 ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.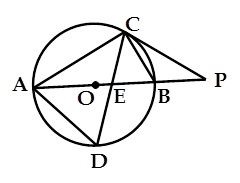
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由;
(3)直接写出CD的长为____________.
相关知识点
推荐套卷
如图,⊙O的直径AB为10,弦BC为6,D、E分别为 ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由;
(3)直接写出CD的长为____________.