如图，在平面直角坐标系中，直线y=2x+b（b＜0）与坐标轴交于A，B两点，与双曲线y=
（x＞0）交于D点，过点D作DC⊥x轴，垂足为G，连接OD．已知△AOB≌△ACD．
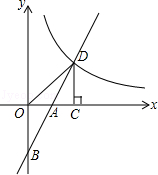
（1）如果b=﹣2，求k的值；
（2）试探究k与b的数量关系，并写出直线OD的解析式．
相关试题
（1）如图①，若∠B+∠D=∠BED,试猜想AB与CD的位置关系，并说明理由。
（2）如图②，要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系？请探索。
推荐套卷
如图，在平面直角坐标系中，直线y=2x+b（b＜0）与坐标轴交于A，B两点，与双曲线y=（x＞0）交于D点，过点D作DC⊥x轴，垂足为G，连接OD．已知△AOB≌△ACD．
（1）如果b=﹣2，求k的值；
（2）试探究k与b的数量关系，并写出直线OD的解析式．
（1）如图①，若∠B+∠D=∠BED,试猜想AB与CD的位置关系，并说明理由。
（2）如图②，要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系？请探索。
粤公网安备 44130202000953号