请阅读下面的材料：计算：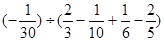
解法一：原式=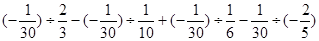
=
=
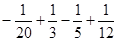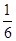
解法二：原式=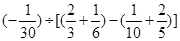
=
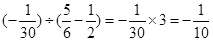
解法三：原式的倒数为（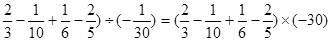
=
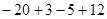=－10， 故原式=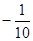
（1）上述得出的结果不同，肯定有错误的解法，你认为解法 是错误的．
（2）请你用你认为简捷的解法计算：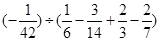
．
x-
=1
÷
，其中x＝
.
÷
－
，其中x＝
－2.相关知识点
推荐套卷
请阅读下面的材料：计算：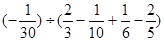
解法一：原式=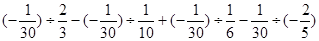
= =
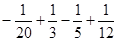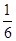
解法二：原式= =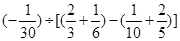
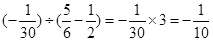
解法三：原式的倒数为（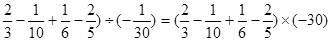
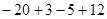==－10， 故原式=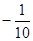
（1）上述得出的结果不同，肯定有错误的解法，你认为解法 是错误的．
（2）请你用你认为简捷的解法计算：．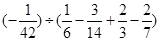
粤公网安备 44130202000953号