如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注: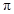 的近似值取3)
的近似值取3)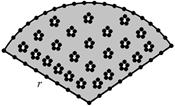
(1)求出S与r的函数关系式,并写出自变量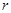 的取值范围;
的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.
相关知识点
推荐套卷
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注: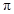 的近似值取3)
的近似值取3)
(1)求出S与r的函数关系式,并写出自变量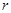 的取值范围;
的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.