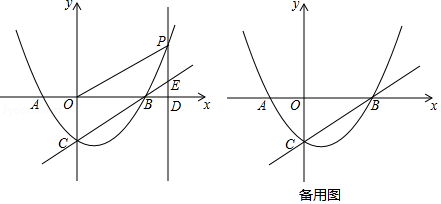
如图，抛物线 的对称轴是直线 ，与 轴交于 ， 两点，与 轴交于点 ，点 的坐标为 ，点 为抛物线上的一个动点，过点 作 轴于点 ，交直线 于点 ．
（1）求抛物线解析式；
（2）若点 在第一象限内，当 时，求四边形 的面积；
（3）在（2）的条件下，若点 为直线 上一点，点 为平面直角坐标系内一点，是否存在这样的点 和点 ，使得以点 ， ， ， 为顶点的四边形是菱形？若存在，直接写出点 的坐标；若不存在，请说明理由．
【温馨提示：考生可以根据题意，在备用图中补充图形，以便探究】
（本小题满分6分）如图，每个小方格都是边长为1个单位长度的小正方形.
（1）将△ABC向右平移3个单位长度，画出平移后的△A1B1C1.
（2）将△ABC绕点O旋转180°，画出旋转后的△A2B2C2.
（3）画出一条直线将△AC1A2的面积分成相等的两部分.
如图，在平面直角坐标系中，直线
与抛物线
交于A、B两点，点A在x轴上，点B的横坐标为－8.
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.
①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG.随着点P的运动，正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标.
如图，在Rt△ABC中，∠B=90°，BC=5
，∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D、E运动的时间是t秒（t＞0）.过点D作DF⊥BC于点F，连接DE、EF.
（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由.
（3）当t为何值时，△DEF为直角三角形？请说明理由.
(10分)某旅行杜拟在暑假期间面向
学生推出“林州红旗渠一日游”活动，收费标准如下：
| 人数m |
0<m≤100 |
100<m≤200 |
m>200 |
| 收费标准(元/人) |
90 |
85 |
75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费10 800元，若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和赳过200人吗?为什么？
(2)两所学校报名参加旅游的学生各有多少人?
与反比例函数
的图象交于点
和
，与y轴交于点C.
=，
=；
＞
时，x的取值范围是；
：
=3：1时，求点P的坐标.
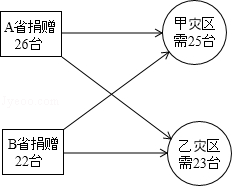
粤公网安备 44130202000953号