（本小題满分12分）如图,直角梯形ABCD中，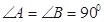
，AD =" AB" = 2， BC = 3，E，F分别是AD,BC上的两点，且AE=BF＝1，G为AB中点,将四边形ABCD沿EF折起到（如图2）所示的位置，使得EG丄GC，连接 AD、BC、AC得（图2）所示六面体．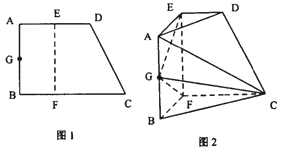
（1）求证：EG丄平面CFG;
（2）求二面角A —CD-E的余弦值．
相关试题
＜1.
+
+
≤3
；
+
+…+
≥n2.
≤
+
.
(参数t∈R）与曲线C：
（参数
∈R）交于A，B两点.相关知识点
推荐套卷
（本小題满分12分）如图,直角梯形ABCD中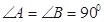，，AD =" AB" = 2， BC = 3，E，F分别是AD,BC上的两点，且AE=BF＝1，G为AB中点,将四边形ABCD沿EF折起到（如图2）所示的位置，使得EG丄GC，连接 AD、BC、AC得（图2）所示六面体．
（1）求证：EG丄平面CFG;
（2）求二面角A —CD-E的余弦值．
粤公网安备 44130202000953号