王华对本校八年级500名学生进行一次每周课余看书时间的抽样调查,结果如下图(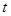 为看书时间)。根据图中提供的信息,解答下列问题:
为看书时间)。根据图中提供的信息,解答下列问题: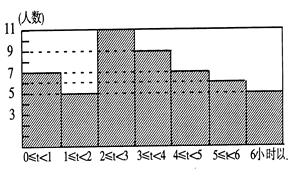
(1)本次抽样调查的学生人数是 人;
(2)每周看书时间在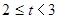 小时这组的频率是 ;
小时这组的频率是 ;
(3)每周看书时间的中位数落在哪个时间段 ;
(4)请估计该校八年级学生每周看书时间不少于4小时的人数是多少人?
相关知识点
推荐套卷
王华对本校八年级500名学生进行一次每周课余看书时间的抽样调查,结果如下图(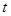 为看书时间)。根据图中提供的信息,解答下列问题:
为看书时间)。根据图中提供的信息,解答下列问题:
(1)本次抽样调查的学生人数是 人;
(2)每周看书时间在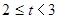 小时这组的频率是 ;
小时这组的频率是 ;
(3)每周看书时间的中位数落在哪个时间段 ;
(4)请估计该校八年级学生每周看书时间不少于4小时的人数是多少人?