如图，在Rt⊿ABC中，∠C=90°，BC=4，AC=8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF，设DE=x，DF=y．
（1）用含y的代数式表示AE；
（2）求y与x之间的函数关系式，并求出x的取值范围；
（3）设四边形DECF的面积为S，求S与x之间的函数关系，并求出S的最大值．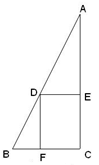
相关试题
，已知线段CD=28㎝，求OP的长。
EB，F是BC的中点，BF=
AC=1.5㎝，求EF的长。
AB，反向延长AC到D，使DA=
相关知识点
推荐套卷
如图，在Rt⊿ABC中，∠C=90°，BC=4，AC=8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF，设DE=x，DF=y．
（1）用含y的代数式表示AE；
（2）求y与x之间的函数关系式，并求出x的取值范围；
（3）设四边形DECF的面积为S，求S与x之间的函数关系，并求出S的最大值．
粤公网安备 44130202000953号