已知圆心在第二象限内,半径为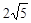 的圆
的圆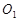 与
与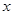 轴交于
轴交于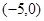 和
和 两点.
两点.
(1)求圆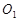 的方程;
的方程;
(2)求圆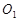 的过点A(1,6)的切线方程;
的过点A(1,6)的切线方程;
(3)已知点N(9,2)在(2)中的切线上,过点A作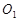 N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线
N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线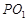 的斜率与直线PN的斜率之积.
的斜率与直线PN的斜率之积.
推荐套卷
已知圆心在第二象限内,半径为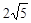 的圆
的圆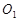 与
与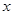 轴交于
轴交于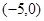 和
和 两点.
两点.
(1)求圆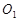 的方程;
的方程;
(2)求圆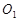 的过点A(1,6)的切线方程;
的过点A(1,6)的切线方程;
(3)已知点N(9,2)在(2)中的切线上,过点A作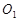 N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线
N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线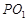 的斜率与直线PN的斜率之积.
的斜率与直线PN的斜率之积.