设定义域为 的函数
的函数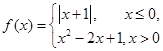
(Ⅰ)在平面直角坐标系内作出函数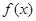 的图象,并指出
的图象,并指出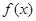 的单调区间(不需证明);
的单调区间(不需证明);
(Ⅱ)若方程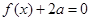 有两个解,求出
有两个解,求出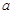 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明).
(Ⅲ)设定义为 的函数
的函数 为奇函数,且当
为奇函数,且当 时,
时,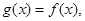 求
求 的解析式.
的解析式.
相关知识点
推荐套卷
设定义域为 的函数
的函数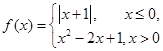
(Ⅰ)在平面直角坐标系内作出函数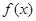 的图象,并指出
的图象,并指出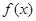 的单调区间(不需证明);
的单调区间(不需证明);
(Ⅱ)若方程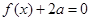 有两个解,求出
有两个解,求出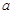 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明).
(Ⅲ)设定义为 的函数
的函数 为奇函数,且当
为奇函数,且当 时,
时,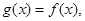 求
求 的解析式.
的解析式.