已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式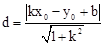 计算.
计算.
例如:求点P(﹣2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x﹣y+1=0,其中k=1,b=1.
所以点P(﹣2,1)到直线y=x+1的距离为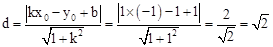 .
.
根据以上材料,求:
(1)点P(1,1)到直线y=3x﹣2的距离,并说明点P与直线的位置关系;
(2)点P(2,﹣1)到直线y=2x﹣1的距离;
(3)已知直线y=﹣x+1与y=﹣x+3平行,求这两条直线的距离.
相关知识点
推荐套卷
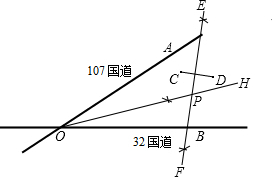
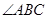 的平分线,AB=AC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N,求证:PM=PN
的平分线,AB=AC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N,求证:PM=PN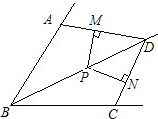
 求
求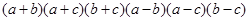 的值。
的值。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号