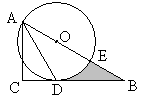
(本小题满分10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D
以AB上一点O为圆心作⊙O,使⊙O经过点A和点D。
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧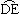 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和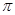 )。
)。
推荐套卷
(本小题满分10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D
以AB上一点O为圆心作⊙O,使⊙O经过点A和点D。
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧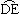 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和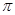 )。
)。