如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.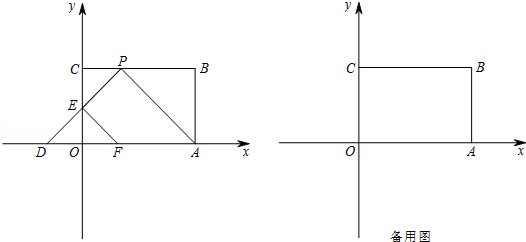
推荐套卷
如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.