（本小题满分8分）如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A（﹣2，2），B（0，5），C（0，2）．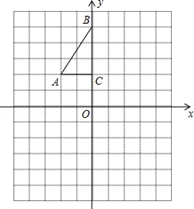
（1）将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形；
（2）平移△ABC，使点A的对应点A2坐标为（﹣2，﹣6），请画出平移后对应的△A2B2C2的图形；
（3）若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标．
相关试题
两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．
（1）(5分)请找出图2中的全等三角形，______________≌______________
并给予证明（说明：结论中不得含有未标识的字母）；
（2）(
3分)证明：DC⊥BE．
中，
，
垂足为E，
垂足为D，
cm，
cm，求
的长．
求证：BE=FC。
求证：△AEF≌△BCD；相关知识点
推荐套卷
粤公网安备 44130202000953号