如图,正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形,将这四个三角形分别沿正方形ABCD的边向外翻折,可得到一个新正方形EFGH.请你在矩形ABCD中画出分割线,将矩形分割成四个三角形,然后分别将这四个三角形沿矩形的边向外翻折,使得图1得到菱形,图2得到矩形,图3得到一般的平行四边形(只在矩形ABCD中画出分割线,说明分割线的作法,不画出翻折后的图形).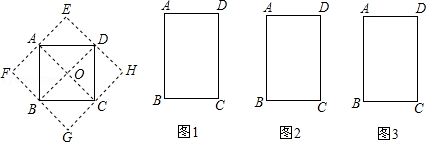
相关知识点
推荐套卷
如图,正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形,将这四个三角形分别沿正方形ABCD的边向外翻折,可得到一个新正方形EFGH.请你在矩形ABCD中画出分割线,将矩形分割成四个三角形,然后分别将这四个三角形沿矩形的边向外翻折,使得图1得到菱形,图2得到矩形,图3得到一般的平行四边形(只在矩形ABCD中画出分割线,说明分割线的作法,不画出翻折后的图形).