我们知道,等腰三角形的两个底角相等,即在△ABC中,∵AB=AC,∴∠B=∠C(如图①所示).请根据上述内容探究下面问题:
(1)如图②,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=90°,动点D在BC边上运动,试证明CD=BE且CD⊥BE.
(2)如图③,在(1)的条件下,若动点D在CB的延长线上运动,则CD与BE垂直吗?请在横线上直接写出结论,不必给出证明,答:_______.
(3)如图④,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=90°,动点D在△ABC内运动,试问CD⊥BE还成立吗?若成立,请给出证明过程.
(4)如图④,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=x°(90<x<180),点D在△ABC内,请在横线上直接写出直线CD与直线BE相交所成的锐角(用x的代数式表示).答:直线CD与直线BE相交所成的锐角______________.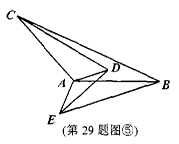
相关知识点
推荐套卷

 粤公网安备 44130202000953号
粤公网安备 44130202000953号