如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
（1）求点D的坐标；
（2）求直线l2的解析表达式；
（3）求△ADC的面积；
（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．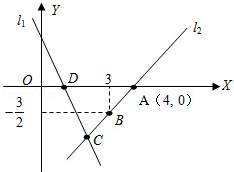
相关试题
（2）
；
；
；
,其中x=－1,y=2.
，AB的中垂线交AB于D，交CA延长线于E，求证：DE=
BC.相关知识点
推荐套卷
如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
（1）求点D的坐标；
（2）求直线l2的解析表达式；
（3）求△ADC的面积；
（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．
粤公网安备 44130202000953号