甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，
以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为
，且各局胜负相互独立.求：
（1）打满3局比赛还未停止的概率；
（2）比赛停止时已打局数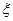
的分别列与期望E.
相关试题
．
的最小正周期；
在
上的值域．
满足：
，且
．
，求证
是等比数列；
都有
成立
．
在区间
上不单调，求
的取值范围；
，存在
，使得
，求
的取值范围．
与直线
相切于点
．
满足的关系式，并用
是椭圆的右焦点，若
是以
为直角顶点的等腰直角三角形，求椭圆
的标准方程
中，
，平面
⊥平面
，
．
平面
与平面
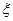所成角的正弦值．推荐套卷
甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，
以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.求：
（1）打满3局比赛还未停止的概率；
（2）比赛停止时已打局数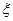的分别列与期望E.
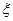粤公网安备 44130202000953号